Machine learning for beginners

Raj Singh
June 23, 2024
05 Mins read
Machine Learning , Neural Networks

Machine learning (ML) is one of the most exciting fields in technology today, powering applications ranging from self-driving cars to image recognition. One of the key architectures driving these advances is the neural network, which mimics the way our brain processes information. If you’re new to machine learning, understanding neural networks can seem challenging, but in reality neural networks are not that complicated

In this blog post, we’ll walk through the basics of neural networks, how they work, and we’ll build a simple neural network using Python and the NumPy library to get you started. This blog post is suitable for a beginner who has no prior knowledge of machine learning and only has basic understanding of Python.

So, let’s start with some basics!

What is a Neuron?

A neuron is the mast basic unit of of a neural network. It takes input, does some math with it and produces the output. A two input neuron would look something like this:

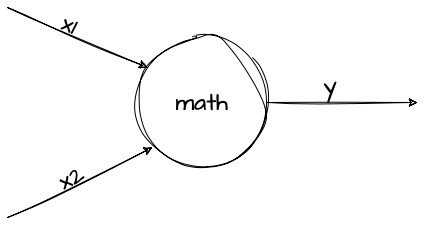
The math includes three steps:

Multiplying the inputs with some weights

$x_1 \to x_1 * w_1$

$x_2 \to x_2 * w_2$
Adding the weighted inputs together and also adding a bias (b)

$\lparen x_1 * w_1 \rparen + \lparen x_2 * w_2 \rparen + b$
Passing the sum from activation function

$f = \lparen x_1 * w_1 + x_2 * w_2 + b \rparen$

Ok, so there are a few unknowns here. Let me explain.

Weights determine the influence input data has on the output product. These are parameters that control the strength of the connection between neurons. They are the neural network’s way of learning from data by capturing the relationships between input features and the target output, allowing the network to generalize and make predictions on new, unseen data. The model learns the best weights during training.
Bias units make networks smarter and more accurate.This is added to the weighted sum to shift the activation function. When there’s no bias, the neural network can’t fit the data well.
Activation Function An activation function is like a decision-making rule for a neuron in a neural network. It takes the input and decides whether that neuron should “fire” (activate) or stay “inactive” (not fire). The function helps the network decide if the input information is important enough to pass along to the next layer.

It is like a light switch where neuron’s input is like the electrical current that goes into the switch and the activation function is like the rule that decides whether the current is strong enough to turn the light on (activate the neuron).

A Commonly used activation function is the Sigmoid function. Sigmoid function converts the input value to an output value in the range (0,1).

With this learning we move on to the next level.

What is a Neural Network?

A neural network is a computational model inspired by the way biological neural networks in the human brain work. It consists of layers of nodes (also called neurons) connected to each other. These networks are used to model complex relationships between inputs and outputs.

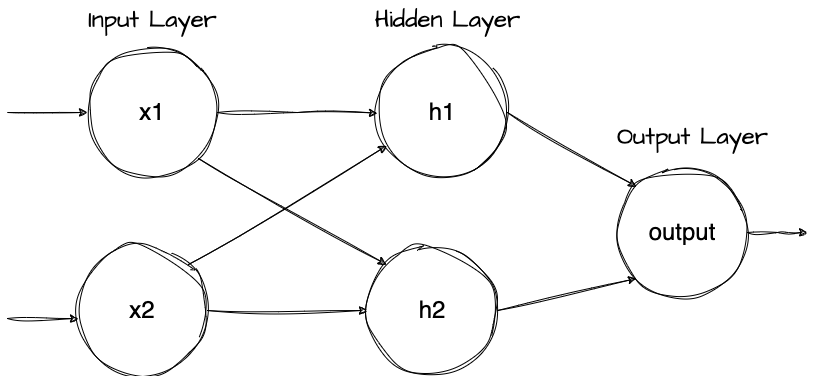
Components of a Neural Network:

Input Layer: The neurons that take in the data features as input (e.g., pixel values of an image, measurements in a dataset).
Hidden Layers: A hidden layer is any layer between the input and the output layer. There can be multiple hidden layers. These are layers where the actual computation happens. These layers help the network learn complex patterns.
Output Layer: The final layer that produces the output: prediction or classification result.

How Neural Networks Work?

Neural networks are trained using a process called backpropagation where:

The model makes a prediction based on the inputs.
The error (difference between predicted and actual values) is calculated.
This error is propagated back through the network, adjusting weights using an optimization algorithm like gradient descent.

Let’s break this down with an example.

Building a Simple Neural Network from Scratch with Python and NumPy

We’ll create a basic neural network with one hidden layer to solve a binary classification problem. For simplicity, we’ll use NumPy for matrix operations.

Step 1: Import Necessary Libraries

import numpy as np

Step 2: Define the Activation Function

We’ll use the sigmoid function as the activation function, which outputs values between 0 and 1, ideal for binary classification.

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

sigmoid(x) computes the sigmoid of x.
sigmoid_derivative(x) is the derivative of the sigmoid function, which is used during backpropagation.

Step 3: Define the Neural Network Structure

We’ll create a simple neural network with:

2 input neurons (features).
1 hidden layer with 2 neurons.
1 output neuron (binary output).

# Seed for reproducibility
np.random.seed(42)

# Number of neurons in each layer
input_layer_size = 2
hidden_layer_size = 2
output_layer_size = 1

# Random initialization of weights and biases
W1 = np.random.rand(input_layer_size, hidden_layer_size)
b1 = np.random.rand(1, hidden_layer_size)
W2 = np.random.rand(hidden_layer_size, output_layer_size)
b2 = np.random.rand(1, output_layer_size)

W1 and W2 are weight matrices connecting the layers.
b1 and b2 are bias terms for each layer.

Step 4: Define the Forward Pass

The forward pass computes the output by passing input data through the network layer by layer.

def forward_propagation(X):
    # Input to hidden layer
    z1 = np.dot(X, W1) + b1
    a1 = sigmoid(z1)  # Activation function for hidden layer

    # Hidden to output layer
    z2 = np.dot(a1, W2) + b2
    a2 = sigmoid(z2)  # Activation function for output layer

    return a1, a2

Here, a1 is the output from the hidden layer, and a2 is the final output of the network.

Step 5: Define the Backpropagation Algorithm

Now, we’ll compute the error and update the weights using the backpropagation algorithm.

def backpropagation(X, y, a1, a2, learning_rate=0.1):
    global W1, W2, b1, b2
    m = X.shape[0]  # Number of examples

    # Compute the error at the output layer
    error_output = a2 - y
    dW2 = np.dot(a1.T, error_output * sigmoid_derivative(a2)) / m
    db2 = np.sum(error_output * sigmoid_derivative(a2), axis=0, keepdims=True) / m

    # Compute the error at the hidden layer
    error_hidden = np.dot(error_output * sigmoid_derivative(a2), W2.T)
    dW1 = np.dot(X.T, error_hidden * sigmoid_derivative(a1)) / m
    db1 = np.sum(error_hidden * sigmoid_derivative(a1), axis=0, keepdims=True) / m

    # Update weights and biases
    W1 -= learning_rate * dW1
    b1 -= learning_rate * db1
    W2 -= learning_rate * dW2
    b2 -= learning_rate * db2

error_output is the difference between the predicted output (a2) and the actual output (y).

We calculate the gradients of the weights (dW1, dW2) and biases (db1, db2) for each layer. These gradients are used to adjust the weights in the direction that minimizes the error, using a technique called gradient descent.

Step 6: Training the Network

Now that we have the forward pass and backpropagation functions, we can train the neural network.

# Training data (X) and labels (y)
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])  # Inputs
y = np.array([[0], [1], [1], [0]])  # Expected outputs (XOR problem)

# Training the network
epochs = 10000  # Number of iterations
for epoch in range(epochs):
    # Forward pass
    a1, a2 = forward_propagation(X)
    
    # Backpropagation and weights update
    backpropagation(X, y, a1, a2)

    # Print the error every 1000 epochs
    if epoch % 1000 == 0:
        loss = np.mean(np.square(a2 - y))  # Mean squared error
        print(f"Epoch {epoch}, Loss: {loss}")

# Final output after training
print("Final output after training:")
print(a2)

Step 7: Visualizing the Output

After training the model for 10,000 epochs, it will be able to approximate the XOR function. The final output should be close to the expected XOR outputs:

For inputs [0, 0] → Output close to 0.
For inputs [0, 1] → Output close to 1.
For inputs [1, 0] → Output close to 1.
For inputs [1, 1] → Output close to 0.

Conclusion

In this post, we built a simple neural network using Python and NumPy to solve a binary classification problem (XOR). We walked through the basic building blocks of neural networks, including forward propagation, backpropagation, and weight updates. By training our network using gradient descent, we were able to improve the accuracy of our predictions.

While this is a very basic example, it lays the groundwork for more complex neural networks. As you gain experience, you can explore more advanced topics such as deep learning, convolutional neural networks (CNNs), and recurrent neural networks (RNNs), or use machine learning libraries like TensorFlow or PyTorch for larger, more complex projects.

Happy coding and learning!

Feel free to experiment with the code and try different activation functions, architectures, or datasets. With practice, you’ll gain a deeper understanding of how neural networks work and how to apply them to real-world problems.